伟大的二级结论

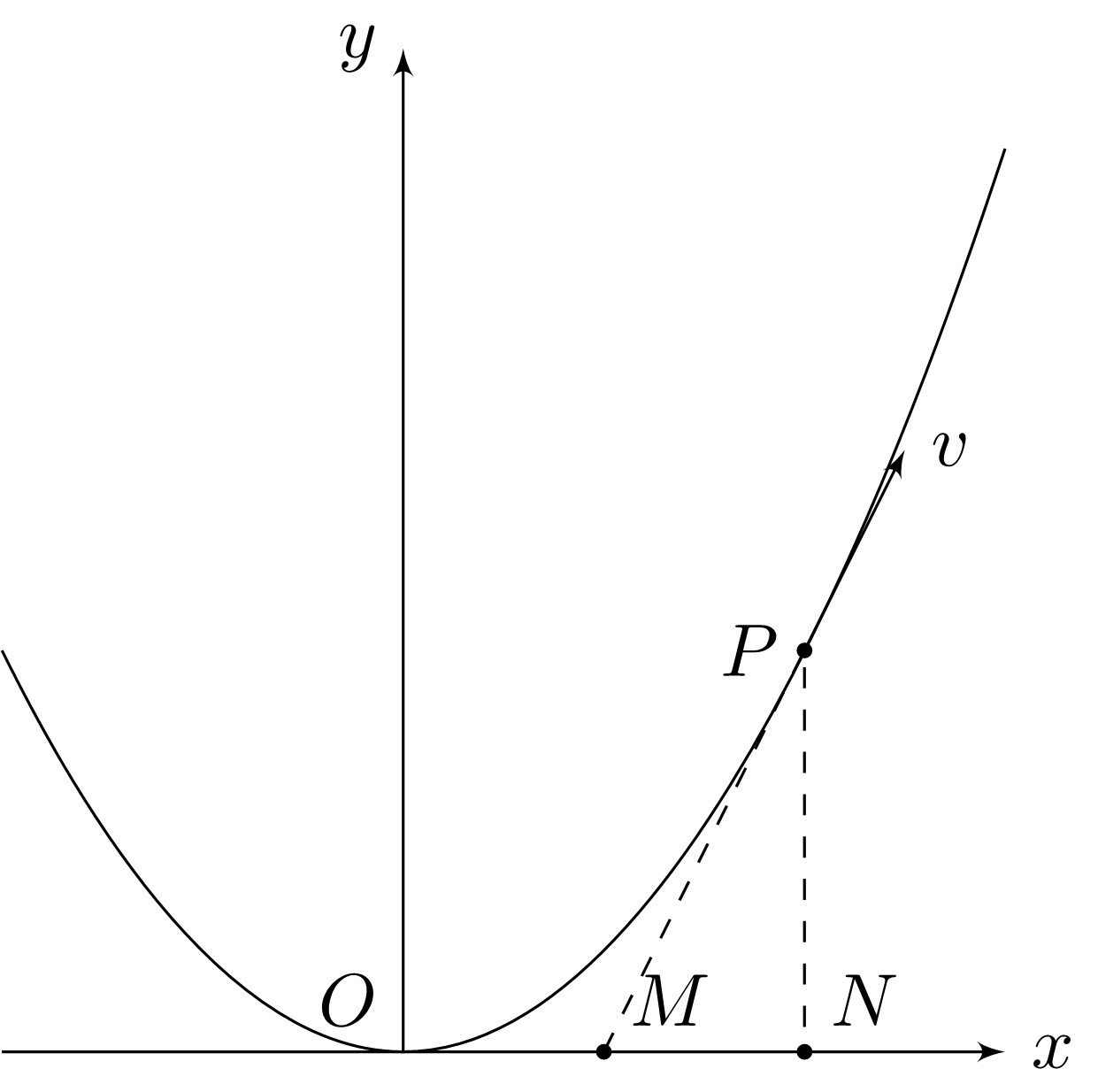
在高中物理运动学中，不难知道平抛运动中有$$\begin{align}x&=v_0t\\y&=\dfrac{1}{2}gt^2\\v_x&=v_0\\v_y&=gt\end{align}$$

分别计算速度偏转角和位移偏转角，可知$$\begin{align}\tan\theta_x&=\dfrac{y}{x}=\dfrac{gt}{2v_0}\\\tan\theta_v&=\dfrac{v_y}{v_x}=\dfrac{gt}{v_0}\end{align}$$

所以就有了伟大的二级结论$$\tan\theta_v=2\tan\theta_x$$

深入思考

经过上述推导，可以得到以下结论（偷个懒，简单点写了）$$\text{轨迹为抛物线}\Rightarrow \tan\theta_v=2\tan\theta_x$$

是个充分条件

不过随便画画其他图象，都不满足这个性质了，随意不免就怀疑上述条件是个充要条件，也即还有$$\text{轨迹为抛物线}\Leftarrow \tan\theta_v=2\tan\theta_x$$

到底是不是呢？

由于最近自己看了看微分方程，也学到了一点东西，所以也弄明白了这个问题

Solution

要证明的命题可以化为$$\dfrac{\text{d}y}{\text{d}x}=\dfrac{2y}{x}$$

整理得到$$\dfrac{1}{y}\text{d}y=\dfrac{2}{x}\text{d}x$$

对两边积分，得(\(C\)为常数)$$2\ln|x|+C=\ln|y|$$

于是$$y=\pm\text{e}^Cx^2$$

由于\(\pm\text{e}^C\in\mathbb{R}\setminus\{0\}\)，所以轨迹必须是抛物线

所以说这是个充要条件，不是吗？

一点收获

所有的幂函数\(y=x^a\)都有这样的性质，在这上面运动的点有（参考点为\((0,0)\)）$$\tan\theta_v=a\tan\theta_x$$

在高中知识水平范畴内，可以证明其充分性，使用高等数学中的微分方程，可以证明其必要性，这是一个非常有意思的结论。

最后一句话

处理未知解析式（或参数方程）的性质时，微分方程真香