例:已知函数\(f(x)=\cfrac{\text{e}^x}{x}(x>0)\),若方程\(f(x)=a\)有两个不等实根\(x_1,x_2\),求证:\(x_1+x_2>2\)
先对\(f(x)\)求导,得\(f'(x)=\cfrac{\text{e}^x(x-1)}{x^2}\),显然,\(f(x)\)在\((0,1)\)上递减,在\((1,+\infty)\)上递增,在\(x=1\)处取得最小值\(\text{e}\)。不妨令\(a=\text{e}\),则可视为\(x_1+x_2=1+1=2\)。
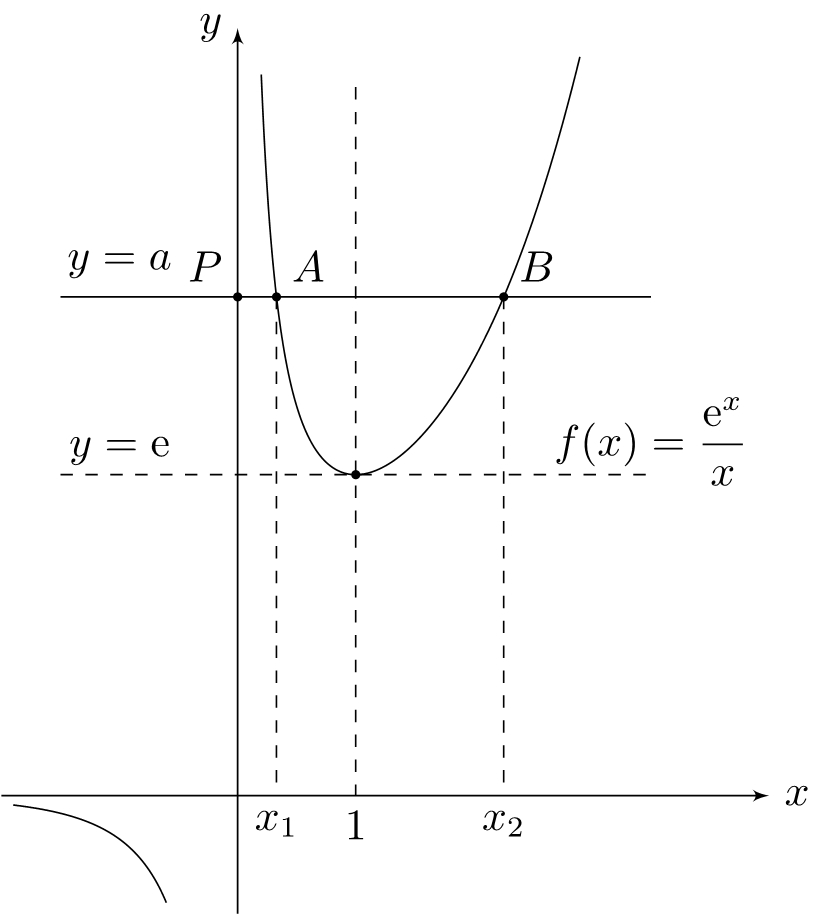
所以此问题一定要从\(x=1\)处入手
由于难以从两根本身入手,于是——极值点偏移,利用函数单调性来间接证明不等关系!!!
首先显然,\(a\in (\text{e},\infty)\)。设两根\(0<x_1<1<x_2\),当\(x_2\geq 2\)时,显然成立。对于\(1<x_2<2\)的情况,构造函数\(g(t)=f(1-t)-f(1+t)\quad(0\leq t<1)\),这里的\(t\)就可以看作偏移量。下证\(g(t)\geq 0\),且当且仅当\(t=0\)时成立:
为计算简便,不妨证明函数\(h(t)=\text{e}^{t-1}(1-t^2)g(t)=(t-1)\text{e}^{2t}+t+1\)在\([0,1)\)上非负,当且仅当\(t=0\)时\(h(t)=0\)即可。
\(h(0)=0\),显然的。
求导,\(h'(t)=(2t-1)\text{e}^{2t}+1\)
\(h'(0)=0\),也是显然的
再求导,\(h''(t)=4t\text{e}^{2t}\),则\(h''(t)\geq 0\),当且仅当\(t=0\)时成立
于是\(h'(t)\)在\([0,1)\)上单调递增,即\(h'(t)\geq h'(0)=0\)
那么\(h(t)\)也在\([0,1)\)上单调递增,即\(h(t)\geq h(0)=0\),\(g(t)\geq 0\),也即\(f(1-t)-f(1+t)\geq 0\)
这时,令\(t\in (0,1)\),则\(f(1-t)>f(1+t)\)。对于满足\(1<x_2<2\)的\(a\),使\(x_2=1+t\),那么$$f(x_1)=f(x_2)=f(1+t)<f(1-t)$$由于\(x_1,1-t\in(0,1)\),结合之前证明过的\(f(x)\)的单调性,可得\(x_1>1-t\),那么$$x_1+x_2=x_1+(1+t)>(1-t)+(1+t)=2$$
证毕








叨叨几句... 1 条评论
难度加深:求证,\(x_1+x_2\)随着\(a\)的增大而增大